گیاهان چگونه از پسِ انجام محاسباتِ ریاضی خود برمیآیند؟
وجودِ سازوکارهای فیزیکی و زیستشیمیایی سبب میشود که الگوی رشدِ دانههای آفتابگردان، از دنبالهی فیبوناچی پیروی کند.
از دانههای گلِ آفتابگردان گرفته تا گلهای گیاهِ کَنگَرِ فرنگی، بسیاری از ویژگیهای دیدهشده در گیاهان، از الگوهایی پیروی میکنند که با جملههای دنبالهی اعدادِ فیبوناچی همخوانی دارد. هر جمله از این دنباله، حاصلِ جمعِ دو جملهی پیش از خود است. به این ترتیب 1، 2، 3، 5، 8، 13… چند جملهی نخستِ این دنبالهی شناختهشده هستند. پژوهشگران نشان دادهاند که پیروی از این الگوها سبب میشود که پیکربندیِ اندامهای گیاهی مانند گلها، برگها و دانهها چنان به صورتِ بهینه شکل گرفته و انباشته شود که گیاهان، بیشترین دسترسی به نور و مواد مغذی را داشته باشند. این موضوع برتریهای دگرگونکنندهای در پی دارد. اما گیاه چگونه درمییابد که به چه ترتیبی باید رشد کند که با این ریختشناسیِ بهینه، همخوانی داشته باشد. بنابر مقالهای که درReview Letters Physical منتشر شده، پیروی از الگوهای فیبوناچی ممکن است نتیجهای از وجودِ سازوکارهای فیزیکی و زیستشیمیاییِ بنیادین و نهفته در روندِ رشدِ گیاهان باشد.
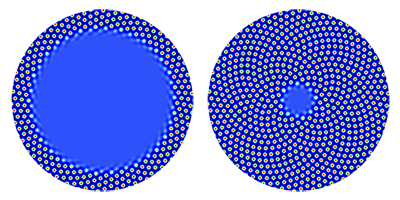
M. Pennybacker and A. C. Newell, Phys. Rev. Lett. 2013
متیو پنیبِیکر (Matthew Pennybacker) و الن سی. نیووِل (Alan C. Newell) از دانشگاهِ آریزونا واقع در توسان، دربارهی سرِ یک گلِ آفتابگردان پژوهش میکنند. دانههای آفتابگردان در این قسمت از گیاه به صورتِ چنبرهای و در پیرامونِ ناحیهای مرکزی رشد میکنند. این ناحیهی مرکزی که در گیاهشناسی به آن «بخشینه» گفته میشود، از سلولهایی تمیزناپذیر ساخته شده است. معمولاً بافتهای گیاهی را با سلولهای ساقهی مو در جانوران مقایسه میکنند. با اضافهشدنِ دانههای تازه، شعاعِ چنبرهها پیوسته کاهش مییابد تا اینکه سرِ آفتابگردان کاملاً پُر شود. به این ترتیب دانههای آفتابگردان به صورتِ خانوادهای از چنبرههای هممرکز، سرِ آفتابگردان را پر میکنند. نویسندگانِ این مقاله از مدلی بهره بردهاند که چگونگیِ پخششدگیِ مادهی «اوکسین (auxin)» در میانِ بخشینه را توضیح میدهد. اوکسین هورمونِ رشدیست که توسطِ گیاهان سنتز شده و به کمکِ پروتیینهای ویژهای، حمل میشود. مناطقی که تمرکزِ اوکسین در آنها بیشینه است، محلِ ساختِ دانههای تازه را تعیین میکنند. شبیهسازیِ این دو پژوهشگر به دقت پیشبینی میکند که دانههای آفتابگردان، چنبرههای ساعتگرد و پادساعتگرد میسازند و اینکه شمارِ این دو دسته چنبره (ساعتگرد و پادساعتگرد)، همواره دو عددِ پیاپی از دنبالهی فیبوناچیست. این یافته چنین پیشنهاد میکند که شاید بتوان بستهبندیهای بهینهای که در سامانهها به وجود آمده را با خانوادهای از معادلاتِ دیفرانسیلِ پارهایِ وابسته به هم، توصیف کرد.
منبع:
http://physics.aps.org/synopsis-for/10.1103/PhysRevLett.110.248104
نویسنده خبر: دلارام میرفندرسکی

 (28 نفر , میانگین : 4,57 از 5)
(28 نفر , میانگین : 4,57 از 5)







انسان چقدر هنوز نادان است
جالبه
سلام
به سوال داشتم ، اگر کسی به رابطه خاصی بین اعداد پی ببره ، از کجا میشه فهمید ک کسی قبل از اون به این رابطه پی نبرده ( ثبتش نکرده ) ؟
با سلام من هم به یک ارتباط بینید میان اعداد که خصوصا. به عدد 22 و … مربوط میشود رسیده ام و توانسته ام که اعداد طبیعی و …را تحلیل و وجود آنها را با شکلی دیگر از ترتیب حال حاضر ،بدست آورم
جالب بود