معرفی فرضیه <گ چ پ ژ> -بخش سوم
بیگ بنگ: شاید طول بکشد به دیدگاه اطلاعاتی در این فرضیه عادت کنید. امروز از شما میخواهم ذهن خود آماده تغییر نگرشی مبنایی کنید. ما در این بخش، ماهیت اطلاعات را بر اساس دایرههای رویداد مرجع، بیان می کنیم. خواهیم دید که زمان و فضای ادراکی چگونه از “زیرفضازمان” اطلاعاتی برمی آید. پیچیدگی ساختار در این مرحله ، ناشی از ذهنیت سه بعدی ما تا کنون است. ولی این پیچیدگی ظاهری ،بسیاری از پرسشهای بنیادین حوزه فیزیک را سر راست خواهد کرد.از اینرو بهتر است همین الان از این پیچ گذر کنید. پس از آن دنیایی از امکانات فراروی شما خواهد بود.
 گفتیم که در جهان ما، حداکثر سرعت ممکن هر سوژه، برابر سرعت نور(C) می باشد. از دیدگاه (گ چ پ ژ)، کوانتوم اطلاعات، سوژه و ناظر را به هم مربوط می کند. دریافت یک واحد اطلاعات، به معنای سفراین کوانتوم از سوژه به ناظر است. اگر سوژه ای از این سریعتر برود، قبل از کوانتوم اطلاعات به ناظر می رسد و رویداد پوچی را می سازد. نمونه کامل یک کوانتوم اطلاعات، فوتون نور است و حداکثر سرعت آن (C) می باشد. اگر سوژه ای با سرعت بیشتر از پشت سر ناظر به عمق پرسپکتیو حرکت کند، از دید ناظر مخفی خواهد ماند.
گفتیم که در جهان ما، حداکثر سرعت ممکن هر سوژه، برابر سرعت نور(C) می باشد. از دیدگاه (گ چ پ ژ)، کوانتوم اطلاعات، سوژه و ناظر را به هم مربوط می کند. دریافت یک واحد اطلاعات، به معنای سفراین کوانتوم از سوژه به ناظر است. اگر سوژه ای از این سریعتر برود، قبل از کوانتوم اطلاعات به ناظر می رسد و رویداد پوچی را می سازد. نمونه کامل یک کوانتوم اطلاعات، فوتون نور است و حداکثر سرعت آن (C) می باشد. اگر سوژه ای با سرعت بیشتر از پشت سر ناظر به عمق پرسپکتیو حرکت کند، از دید ناظر مخفی خواهد ماند.
از اینرو ” دایره رویداد ” را برای نشان دادن یک “تغییر” در یک “رویداد کامل” با شعاع برابر با شعاع جهان ، به کار میبریم. ساختار هندسی و جبری اطلاعات در این فرضیه، بر اساس تناظرهای گفته شده ، بر مبنای ” دایره رویداد ” خواهد بود. در ادامه خواهیم دید که از دیدگاه این فرضیه، کوانتومهای اطلاعاتی در این دایره های رویداد قابل تعریف هستند. از اینرو ساختار هندسی دایره های رویداد زمانی را معادل نوعی ” فاز پیش هندسی” از جهان میدانیم. تعامل کوانتومهای متناظر در این” فاز پیش هندسی “(pregeometric phase )، اطلاعات قابل پردازش (مثل زمان قابل ادراک) در جهان هندسی را تعریف میکند.
روند ادراک به این شرح است:
ما سوژه ای را می بینیم که با سرعت v حرکت میکند.در این مرحله (پیش آگاهی) سوژه ای را تعریف میکنیم که با سرعت v به مقدارdx جابجا میشود.( توجه کنید که هنوز مفهوم زمان و جابجایی در مرحله ادراکی را تعریف نکرده ایم). فاصله سوژه تا مبدا فرضی ساکن را برابر شعاع مرجع چD میگیریم. مقدار جابجایی منتسب به این سوژه برابرdx خواهد بود. این جابجایی فرضی، بیانگر سرعت سوژه است.
(از اینرو اطلاعات در مرحله پیش آگاهی شامل اینها است: جابجایی dx, زمان tx که براساس سه پارامتر مبنایی قابل تعریف هستند: سرعت v ،زمان مرجع جهانی چt و حداکثر سرعتc
نمیخواهم گیج شوید، ولی در گوشه ذهن خود داشته باشید که در مرحله پیش هندسی آگاهی، با اطلاعات مبنایی طرف هستیم. بعدا خواهیم دید که با توجه به ساختار هندسی اطلاعات در مدل این فرضیه، چگونه هر ادراک در مرحله پیش آگاهی به زمان مرجع جهانی مربوط است)
۳-متناسب با این جابجایی فرضی، زمان فرضی tx را تعریف میکنیم.
۴-گذشت زمان و جابجایی مکان ادراکی d و tΔ ، محصول جابجاییهای زمانی- فضایی پیش هندسی(tx,dx) خواهد بود.
d و tΔ بازه زمان و مکان ادراک شده توسط ناظر را نشان میدهند که به نسبت شعاع جهانی بزرگ شده است. مهم نیست حرکت سفینهای با سرعت ۹۰% سرعت نور را یک دقیقه دنبال کنید یا یکسال. زمان و مکان به نسبت سرعت در مقیاس جهانی ،بزرگ شده و تحلیل می شوند.
مثلا برای رویداد دور شدن سفینه فوق، دایره رویدادی با شعاع چD را رسم می کنیم که سوژه ۹۰% آنرا (dx)طی کرده است
معادله ۱
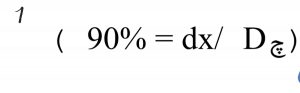
تحلیل زمان:
می توان همان شکل هندسی دایرهای را برای زمان هم رسم نمود. با این تفاوت که مقیاس ها طولی نیستند.
همچنین باید رابطه فضا – زمان را در نظر داشت.
در این فرضیه بردارهای محوری “تغییر در محور فضایی dx=مقدار حرکت “، همواره بر بردار محور ” تغییر در محور زمانی =گذشت زمان tx عمود خواهد بود. اگر به ساختار دایره رویداد توجه کنید می بینید که اگر dx را در جهت شعاعی تعریف کنیم، میتوانیم زمان را به میزان چرخش میله نامرئی مربوط کنیم. مدار دایره همواره برشعاع آن عمود است. چرخش به میزان زاویه مرکزی آلفا در زمان tx روی میدهد. بردار tΔ به روی محیط دایره در نقطه a مماس است. از اینرو بر محور شعاعی فضاگونه، عمود است.( شرط تعامد بردارهای مختصات)
خواهیم دید که برعکس در دایره زمانی، محور شعاعی” زمان گونه” است. در شکل ۴. ه، دایره رویداد نزدیک شدن دوسوژه ( یکی متحرک در پوسته و دیگری ساکن در مرکز) نشان داده شده است بردار حرکت dx به روی محیط دایره زمانی است و بردار جابجایی ادراکی ناظر d ،در نقطه a مماس خواهد بود.
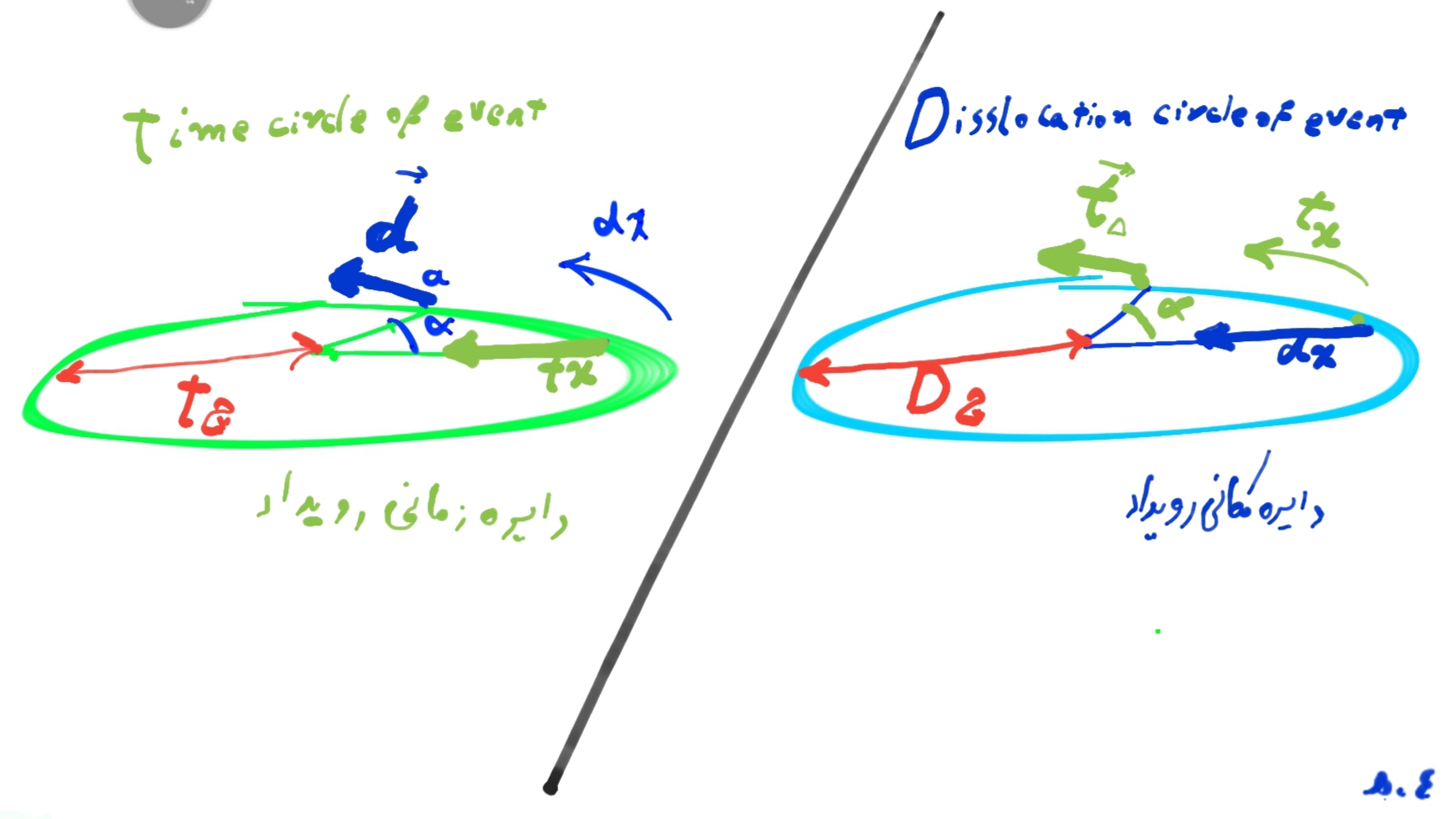
اینکه چرا شعاع دایره را به شعاع جهان رساندیم، به دلیل بیان حرکت سوژه به شکل حرکت یک ” کوانتوم اطلاعاتی ” است. حرکتی که بر مبنای حرکت مرجع ( شعاع جهان ) بنا شده است. سوژهای که با سرعت v حرکت میکرد، حالا به شکل کوانتومی با سرعت نورc متناظر خواهد بود. مسافت dx متناظر است با فاصلهای که” سوژه موهومی”(شبه ذره اطلاعات) در زمان tx و با سرعت نور طی کرده است.
شعاع دایره رویداد فضایی را چD نامیدیم. حالا در دایره زمانی، شعاع چt را معرفی می کنیم:
1_زمان لازم برای سوژه ای با سرعت نور در طی کردن dx
dx/c=tx
۲_زمان لازم برای سوژه در طی کردن شعاع جهان با حد اکثر سرعت (نور)
معادله ۲

در دایره فضاگونه، شعاع برابر چD بود. dx اینگونه تعریف می شود:
مقدار جابجایی سوژه با سرعت v که در زمان مرجع چt روی میدهد.
معادله ۳
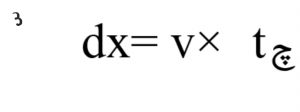
بنابراین داریم :
معادله ۴
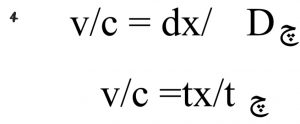
با تبدیل دایره مکانی به زمانی، بردار حرکت dx را عمود بر شعاع (مماس به روی محیط دایره بزرگ زمانی چt ) تعریف می کنیم. با توجه به تناظر چرخشی، بردار tz نیز به روی بردار حرکتی dz عمود می باشد. از این رو tz را به روی شعاع دایره ای تعریف می کنیم که بردار مکانی dz محیط دایره قرار دارد.
دو دایره، دو ناظر:
برای بیان کامل حرکت سوژه ای در سه بعدی، باید دو ناظر فرضی را تصور کنیم که هر یک می تواند اطلاعات حرکت در سطح روبه خودش را بلافاصله با ناظر اول شریک شود. از دیدگاه این فرضیه، یک “رویداد کامل”، حاوی دو سطح اطلاعاتی خواهد بود. هر ناظر یک سطح ادراکی _ اطلاعاتی مربوط به خودش را دارد. در واقع، در هر رویداد، یک ناظر فرضی بیشتر وجود ندارد که میتواند دو سطح ادراکی را همزمان ببیند. این ناظر فرضی از بعد پنجم به روی چهاربعدی رویداد، مشرف است. او اطلاعات دو سطح عمود بر هم را همزمان درک می کند. بعدا در اینباره بیشتر خواهیم گفت. در شکل ۴.ی موقعیت دو ناظر و سطح ادراکی رو به آنها را میبینید. هر ناظر با تعریف دایره رویداد، اطلاعات سطح رو به خودش را در یک دایره مرجع جهانی، دریافت می کند.

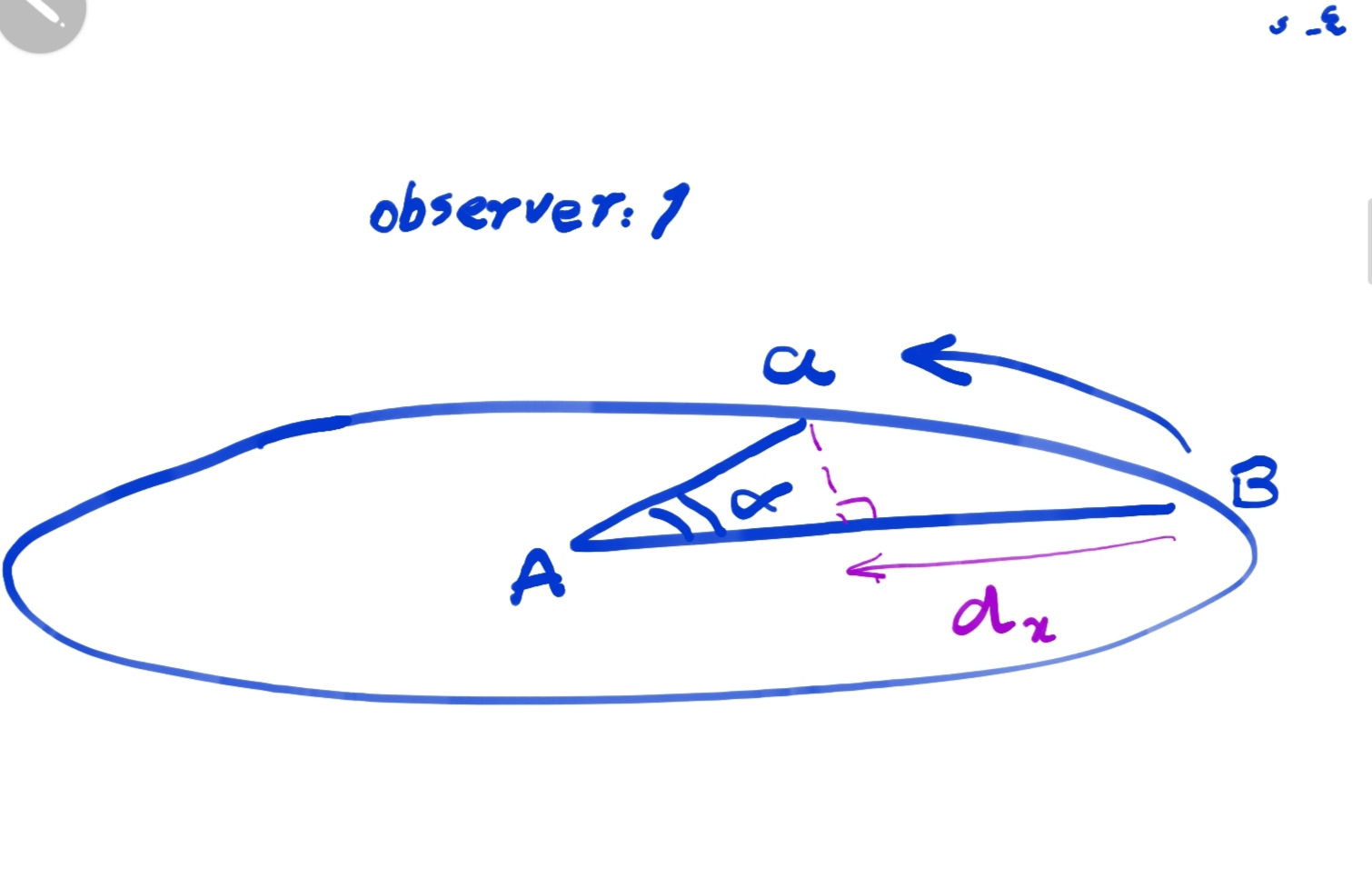
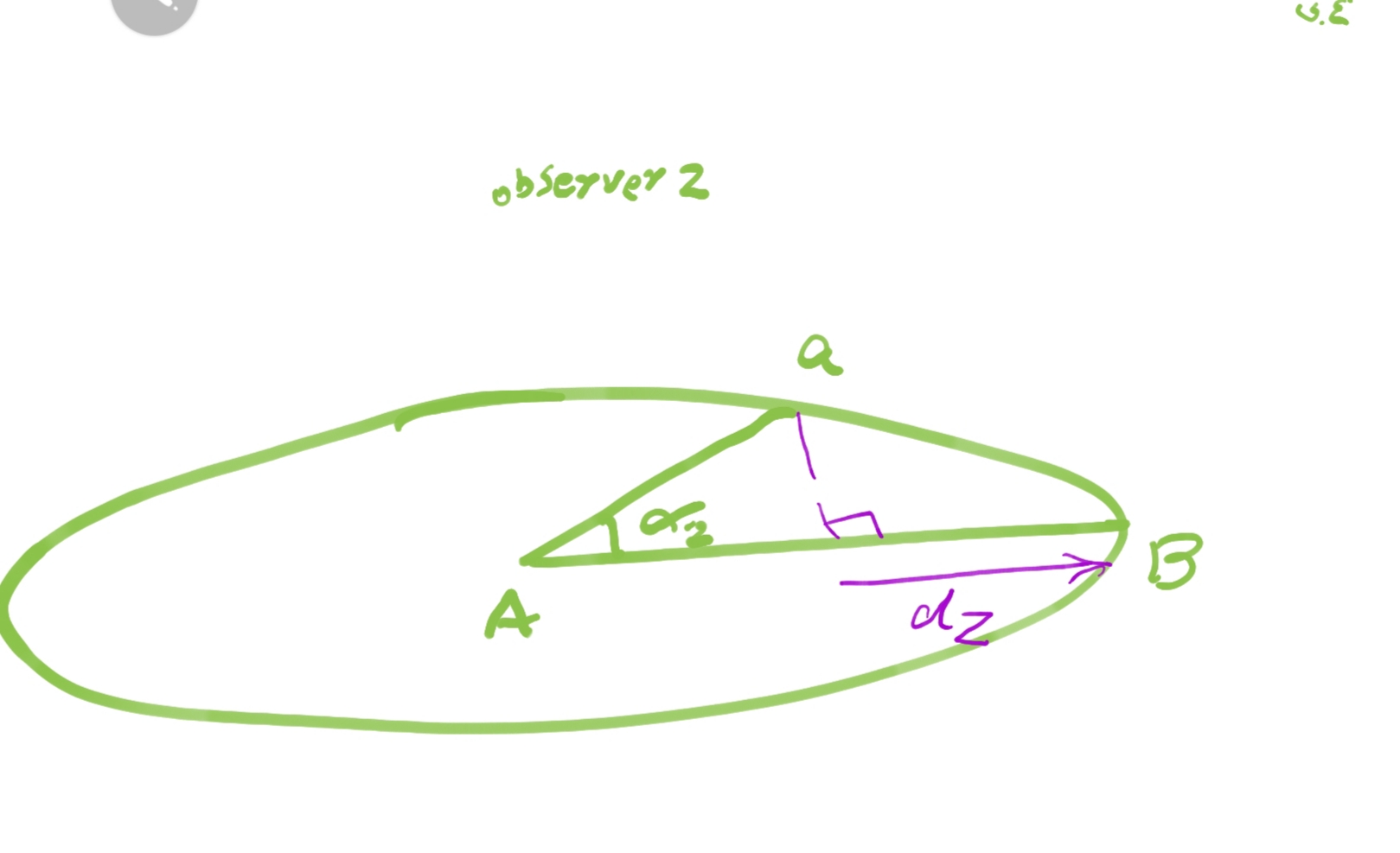 مسئله اینجاست که ما ناظرانی هستیم که سه بعد فضایی و یک بعد زمانی را درک میکنیم. حالا باید عادت کنید که این دیدگاه چهاربعدی را به شکل دیگری ببینید: دو بعد” فضاگونه” ، و “دو بعد زمان گونه”. هر” بعد شعاعی فضاگونه” و “بعد مداری زمان گونه”، یک دایره رویداد را بیان می کند. دو دایره رویداد متناظر خواهیم داشت.
مسئله اینجاست که ما ناظرانی هستیم که سه بعد فضایی و یک بعد زمانی را درک میکنیم. حالا باید عادت کنید که این دیدگاه چهاربعدی را به شکل دیگری ببینید: دو بعد” فضاگونه” ، و “دو بعد زمان گونه”. هر” بعد شعاعی فضاگونه” و “بعد مداری زمان گونه”، یک دایره رویداد را بیان می کند. دو دایره رویداد متناظر خواهیم داشت.
● از دیدگاه <گ چ پ ژ>، این تغییر نگرش، امری جدی است. اطلاعات به شکل دیفرانسیل، در یک کوانتوم <ژ> خلاصه می شود، و به ادراک در می آید. این فرایند فشرده سازی اطلاعات و پردازش آن توسط ناظر، تعریف جبری و هندسی ویژهای دارد که در ادامه می آید.
● آنچه ما پردازش می کنیم، ساختاری چهار بعدی است. دو سطح دو بعدی از اطلاعات. برای درک بهتر به مثال زیر توجه کنید:
سفینهای با مسافران عصبانی که با هم می جنگند. هر گروه به یک سمت تکیه داده و به سمت مقابل تیراندازی می کند. یک ناظر در عقب_ جلو سفینه میتواند مسیر تیرهای شلیک شده را ببیند. برای درک کامل رویداد باید ناظری دیگر را هم در نظر بگیرید که سفینه را به شکل سوژه در حال حرکت می بیند. او که قضیه را نمیداند، مسافرانی آرام را می بیند که به پشت تکیه دادهاند و با سرعت به جلو می روند. یکی از آنها اطلاعات درون سفینه را می بیند و دیگری اطلاعات بیرونی را. برای تعریف رویداد کامل “تغییرات سفینه”، دو دایره رویداد عمود بر هم نیاز داریم. این دو رویداد درونی و بیرونی هرکدام گوشهای از رویداد حرکت سوژۀ فعال را نشان می دهند. بعدا به تفاوت اطلاعات درونی وبیرونی اشاره خواهم کرد.
تغییر بیرونی معادل حرکت سوژه صفر بعدی روی محور تک بعدی است. مثلا حرکت سفینه نسبت به ناظر ساکن. تغییر داخلی شامل حالات درون سوژه است که در مبحث ترمودینامیک به آن اشاره می شود. مثلا رویداد تیر اندازی در داخل سفینه.
توجه کنید که دیدگاه “وجود دو مقطع متناظر عمود بر هم ” در مورد هر تغییر وجود دارد. مثلا رویداد حرکت سفینه نقطه ای روی محور فضا زمان را در نظر بگیرید. همانطور که گفتیم
سوژه با سرعت v در یک زمان مفروض t پیش می رود. ناظر در ابتدا آنچه دریافت می کند را مفروض می گیرد: “سرعت”. یعنی “نسبت تغییر فضایی به تغییر زمانی( گذشت زمان) ” و این اطلاعات پایه است. همانطور که در نسبیت، فضا زمان در اثر سرعت تغییر می کنند، در اینجا نیز سرعت سوژه را معادل اطلاعات پایه میدانیم. ناظرها در چارچوب های ساکن و متحرک نسبت به هم، روی” سرعت” توافق خواهند داشت.
بعد از این، هر ناظر فضا زمان خود را اندازهگیری می کند. فعلا کارمان راحت تر است. چون در هر دو دایره رویداد از یک تغییر( داخلی_ خارجی) اطلاعات میگیریم . مثلا برای حرکت خارجی سفینه، دو ناظر فرضی ساکن را عمود بر دو صفحه در نظر میگیریم. هر کدام یک سطح عمود بر دیگری دارد. یکی حرکت سفینه را رو ی خط صاف میبیند و دیگری تغییر اندازه یک ضلع از سطح رو به خود را می بیند.
مثلا اگر سطح مقطع سفینه به شکل مربعی به ضلع L باشد، برای تحلیل حرکت ( دور_ نزدیک شدن سفینه)، دایره رویدادی را تعریف میکنیم که در آن یک سر ضلع نامرئی ساکن و سر دیگر آن متحرک است. در اینجا طول شعاع نامرئی دایره را به شعاع جهان می رسانیم و تغییر dz را در دایره رویداد اطلاعاتی به شکل L بیان می کنیم. این رویداد درونی سفینه خواهد بود.( کسی که بر سطح مقطع مربعی سفینه مشرف باشد، میتواند تیراندازی را ببیند)
فضای تغییر اطلاعاتی مبنایی، فضایی با دو سطح متناظر بیرونی – درونی است. فضایی چهار بعدی: دو دایره فضایی_ زمانی. در هر دایره، شعاع زمان گونه و مدار فضاگونه ( و یا بالعکس) است. اینها دایرههایی فرضی هستند که حرکت مشاهده شده با سرعت v را به چرخشی به میزان آلفا متناظر کردهاند.
حتی در تحلیل یک حرکت بیرونی هم دو ناظر فرضی وجود خواهند داشت. ایندو دایره هایی متناظر را می بینند. ناظر اطلاعات زمانی -مکانی را از هر دو دایره می گیرد.
** تفاوت ایندو دایره بنیادین است: جهت حرکت عقربه نامرئی در دایرهای متناظر، معکوس یکدیگر است. یکی از آنها گذشته نگر و دیگری آینده نگر است. (این دو دایره فرضی به روی هم عمود هستند و حافظ شرط تقارنهای فیزیکی خواهند بود. در نهایت ساختاری خواهیم داشت که تقارنهای CPTو وابسته را درخود دارد)
اگرچه اینها دایره های اطلاعاتی فرضی هستند، ولی با دنیای واقعی به شکل روابط ریاضی مرتبط هستند. این ساختار و این روابط، پایه بیان <گ چ پ ژ> است.
ساختار دایره های رویداد متناظر در دل هم:
همانطور که دو بردار فضایی dx و dz وجود دارند، دو بردار زمانی tz و tx وجود دارند. ایندو بردار زمانی، سطحی را میان خود بیان می کنند که متناسب با “زمان ادراکی رویداد” است. ما زمان را به شکل دیفرانسیلی(گذشت زمان) میبینیم . این بردار ، محصول مشترکی است از زمان tx و tz که به شکل موهومی در دایره های متناظر حضور دارند. توجه کنید که در <گ چ پ ژ>، با اطلاعات به شکل ریاضی سر و کار داریم. ساختار ریاضی تنها مبنای ممکن برای پردازش و درک اطلاعات است. درست مانند فرایند رمزگزاری و رمزگشایی.
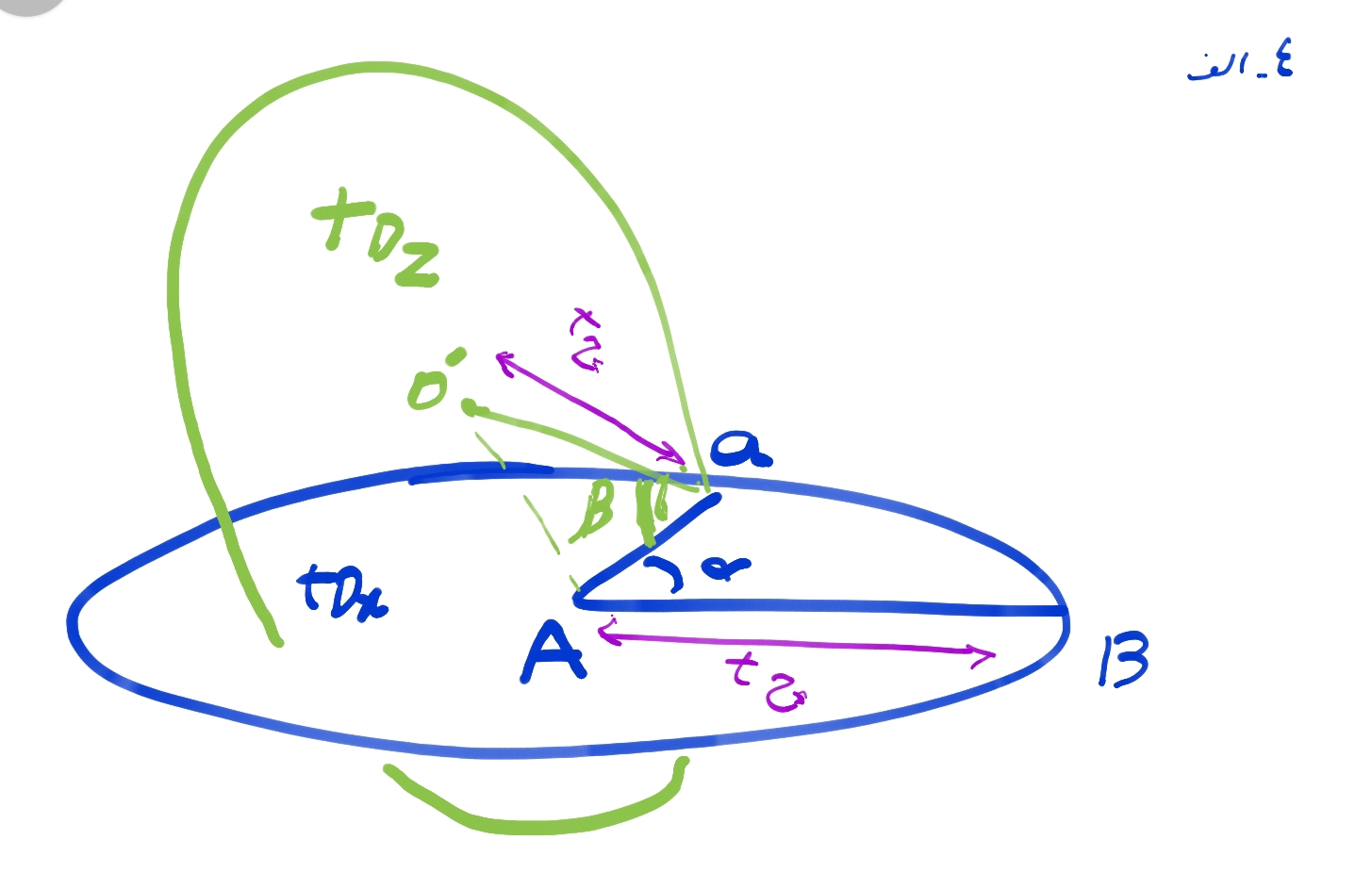
تا به اینجا از وجود دو دایره ادراکی گفتیم که بر هم عمود هستند خواهیم دید که محل برخورد محیط دو دایره با هم(نقطه محیطی a در شکل ۴_الف)، محل اعمال “بردار زمانی دیفرانسیلی ادراکی” می باشد.( اگرچه این بردار به روی دایره مکانی رویداد قرار دارد، ولی با توجه به تناسب دایره های مکانی با زمانی، این بردار را به روی دایره زمانی تعریف میکنیم تا رابطه بردارهای زمانی مشخص تر شود)
هرکدام از بردارهای زمان گونه، به روی شعاع مرجع دایره ای قرار دارند که بر دایره اول عمود است. اگر دایره زمانی اول را tDx بنامیم، دایره دوم tDz خواهد بود. این دو دایره بیانگر دو دایره رویداد در دو سطح عمود بر هم( در واقع غیر مماس) است. در شکل ۴ رابطه این دو دایره را با هم می بینیم.
( توجه کنید که همه تحلیلها را برمبنای دایره زمانی انجام میدهیم. چون همواره در دو دایره ، tx=tz , دایره ها کاملا مشابه خواهند بود و تقارن وجود خواهد داشت)
زمان در (گ چ پ ژ):
در دیدگاه این نظریه، آنچه به عنوان زمان در فرمول های فیزیکی بروز می کند، برداری است که معادل میانگین هندسی tz و tx می باشد. هر بردار به یک “زیر محور شعاعی” اشاره دارد. آنچه ناظر به عنوان زمان رویداد ادراک می کند، نوعی پنجره زمانی است. معادل برداری که حاوی اطلاعات تغییر در هر دو دایره است. توجه کنید که اگرچه تغییر در هر دو بعد dx و dz همیشه در یک سوژه با هم برابر نیست؛ ولی ما در اینجا با “سوژه نقطهای” سروکار داریم تا یک حرکت را بیان کنیم. در دو دایره مشابه ،dx و dz در اینجا برابر گرفته می شوند. اما تغییر _ گذر زمان منتسب به هر دو بعد، در همه شرایط برابر است. ما از تغییری حرف می زنیم که در هر دو بعد به شکل همزمان و در دوره ای مشخص روی داده است.
(tx= tz)
برای روشن شدن مسئله به مثال میله نامرئی با دو سر رنگی برمیگردیم. این میله با طول L اگر به مقدار چD دور شود، از دید ناظر ناپدید می شود.
در این حالت حداکثر حرکت در جهت ادراکی، برابر طول میله است.
dx=L
اما در همین حال، ناظر دیگر، این حرکت را به روی سطح ادراکی خود، برابر شعاع جهان چD می بینند. در تحلیل زمانی، مهم این است که زمان تغییر برای هر دو حرکت متناظر را برابر قرار می دهیم. همچنین گفتیم که در تحلیل یک حرکت نیز، دو دایره غیر مماس و با ابعاد متناظر خواهیم داشت. اینها “زیرفضای ادراکی” را برای یک رویداد تشکیل می دهند.
زاویه β:
بردارهای یکه tz و tx در اندازه با هم برابرند. زاویهβ، زاویه میان دو بردار tz و tx است. جهت بردار (tΔ ) ⃗ با قانون دست راست تعیین می شود. با دست چپ به بردار معادل در جهت مخالف می رسیم. از این به بعد، منظور از دایره رویداد (دایره ای ادراکی)، همین دایره زمانی است. در شکل ۴.ب نقطه محیطی a محل اعمال بردار زمانی ادراکیtΔ است.
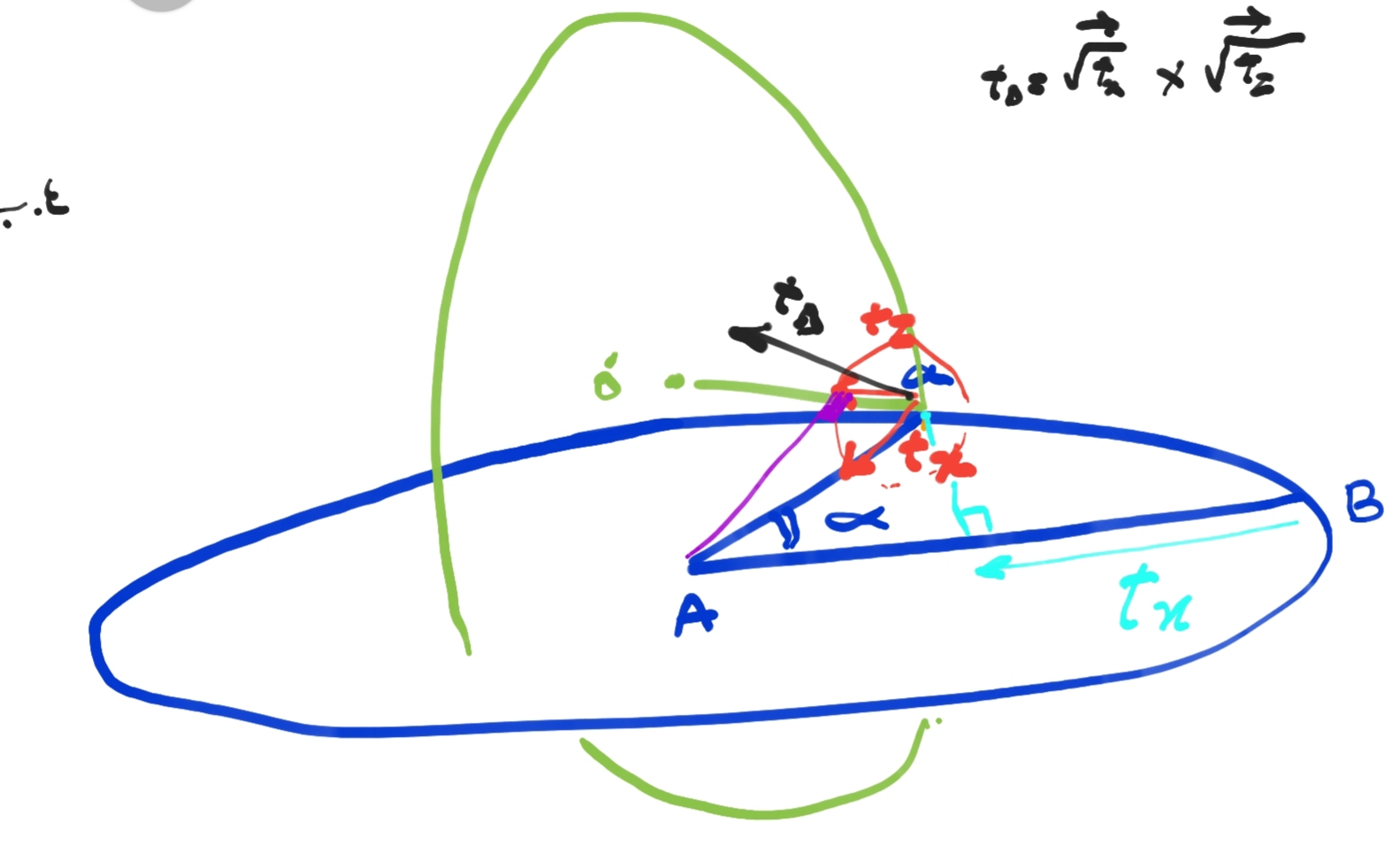
نکته اینجاست که ناظر از هر دو سطح متناظر ،اطلاعات را دریافت میکند. ساختار اطلاعات شعاعی هر دایره از دید او تنها یک بعد دارد. ولی او اطلاعات را دو بُعدی و در سطح پردازش می کند. هر بردار زمانی شعاعی، مبنای پیش هندسی اطلاعات است. از اینرو این “زیربردار “ها را زیر رادیکال بیان می کنیم. حاصلضرب برداری این دو زیر بردار مبنایی، بردار زمان tΔ در فاز ادراکی خواهد بود.
در اینجا میتوان سطح پنجره زمانی که معادل با بردار گذر زمانی tΔ است را بیان کرد:
معادله ۵

سطح مثلث محصور میان بردارهای زمانیStرا در شکل ۴.ج می بینید.
ساختار ادراکی رویداد:
برای درک ساختار ادراکی رویداد، باید همه جنبه های متناظر رویداد را در دو دایره زمانی در نظر داشت. از این رو دایره زمانی tDz و tDx را تعریف می کنیم.
شعاع این دو دایره با هم برابر است : tDx =tDz = چt
با توجه به شکل 4.ج، برای رسم ساختار زمانی رویداد، به این روش عمل می کنیم:
1- دایره tx را به شعاع چt و به مرکزیت A رسم می کنیم. فرض کنیم که حرکت به میزان زاویه α ̅آلفا اتفاق افتاده است، بنابراین به نقطه محیطی a می رسیم.
2- به مرکز نقطه a، دایره ای به شعاع tz=tx رسم می کنیم. به صورتی که سطح مقطع آن بر سطح مقطع دایره tDx عمود باشد. این دایره کوچک tz خواهد بود.
3- از نقطه A بر دایره کوچک tz ،مماس را رسم می کنیم.
4- از نقطه برخورد این مماس با دایره کوچک tz، شعاع دایره ( بردارtz )را رسم می کنیم. بردار tx به مبدأ α و به سمت A رسم می شود.
5- از نقطه α در امتداد پاره خط tz، و به طول چt رسم می کنیم( ادامه میدهیم) تا به نقطه ‘Oبرسیم که مرکز دایره tDz می باشد.
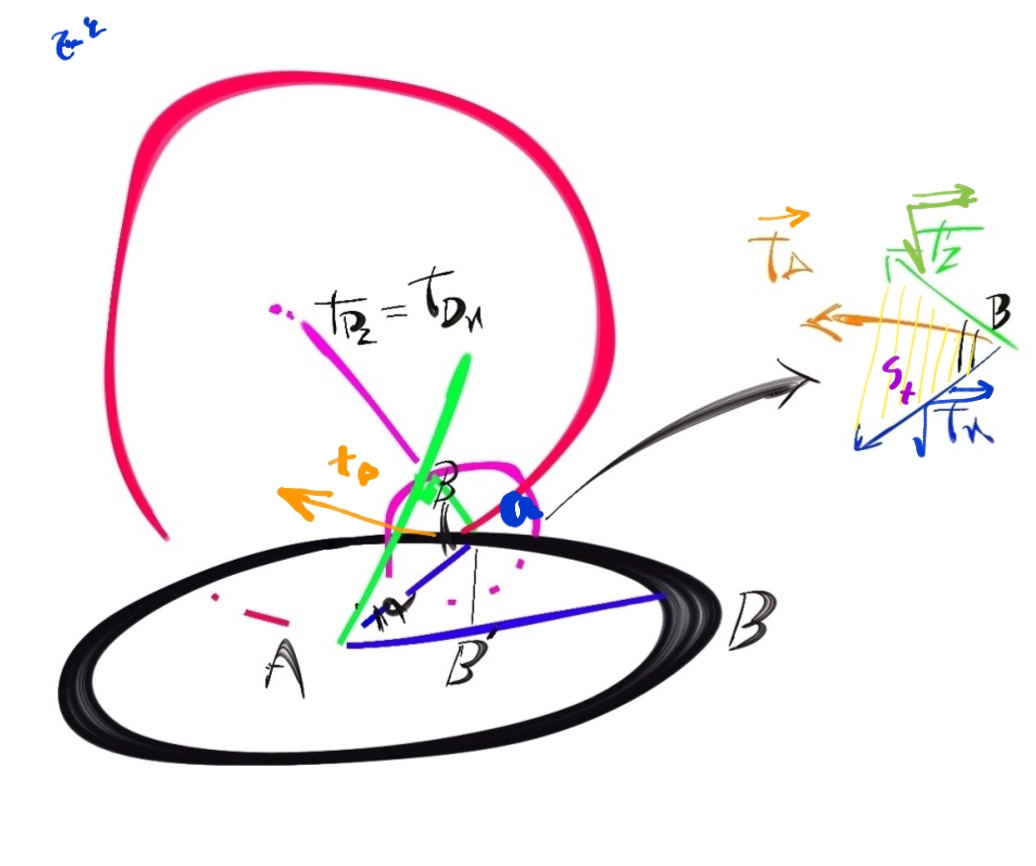
در این مرحله، زاویه ( B) ̂ تعریف می شود.
معادله ۶
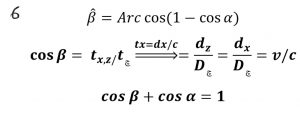
معادله بالا ساختار مبنایی هندسه اطلاعات و رابطه دایره های رویداد را با هم بیان می کند و در تحلیلهای دیگر نیز استفاده می شود. از این به بعد باید عادت کنیم که مفاهیم اطلاعات را به شکل زوایا ببینیم. بر اساس آنچه گفته شد، تغییر فضا زمان ادراکی را برای دو ناظر ساکن _ متحرک مقایسه می کنیم.
نسبیت خاص:
اگر سرعت نسبی دو شیئی صفر باشد یا نسبت به هم ساکن باشند:
معادله ۷
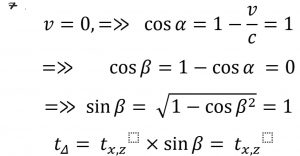
ولی اگر سرعت نسبی برابر V وجود داشته باشد:
معادله ۸
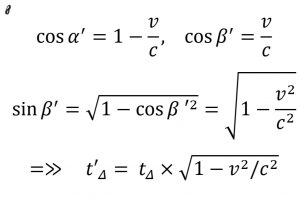
از اینجا می توان ضریب اتساع زمان را تعریف کرد:
معادله ۹
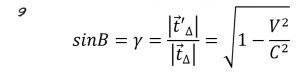
اطلاعات پایه به شکل “گذر زمان” درک می شوند. از این به بعد به جای فاز پیش هندسی اطلاعاتی، جهانی سه بعدی ادراک می شود که در زمان پیش می رورد. درست مانند “زمان ادراکی ” ، “جابجایی ادراک شده d “هم تعریف می شود. با توجه به اینکه ناظر تنها به محور dx در سطح اطلاعاتی خودش مشرف است،dz را نمیبیند. ولی ناظر دیگر میتواند کوچک شدن سطح سفینه را ببیند. او dz را به عنوان جابجایی می بیند. او سرعت دیگری را به جایv درک می کند. توجه کنید که ناظر نسبت بین ابعاد ادراکی فضا زمان ادراکی خود را به شکل سرعت نور بیان می کند. او سرعت v را به شکل اطلاعات اولیه در فاز پیش هندسی دریافت می کند. مانند نسبیت، ناظرها در چارچوبهای متفاوت بر سر سرعت توافق خواهند داشت. با توجه به رابطه تبدیلی زمان و مکان:
tΔ=d/c
بردار زمانی ادراکیtΔ روی زیر-دایرههای مکانی، مماس است. بردار d نیز نسبت بر زیر-دایره های زمانی، مماس است. ولی با توجه به رابطه چرخشی- شعاعی( شرط تعامد محورهای فضایی-زمانی) این بردارها با هم دایره رویداد برایند را خواهند ساخت. بعدا به این میپردازیم.
با دیدن یک سرعت مشخص v حال می توان اثر انقباض طول را دید:
معادله ۱۰
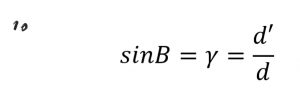
نسبیت عام:
این بار، به جای محاسبه تأثیر سرعت بر انقباض طول (اتساع زمان)، تأثیر شتاب را بیان می کنیم.
از آنجا که حرکت سوژه به روی شعاع ،خطی است، داریم:
معادله ۱۱

اگر شتاب حداکثر را به گونه ای بیان کنیم که سرعت اولیه برابر صفر و سرعت نهایی برابر c باشد، معادل این است که کوانتوم ساکن سوژه از مرکز به پوسته دایره رویداد برسد.طبق قانون هابل ،سرعت از 0 به c می رسد. در این حالت تغییر مکان برابر شعاع دایره رویداد است. بعدا خواهیم دید که این رویدادی است مشابه دایره جهانی ولی با w سرعت زاویه ای متفاوت. سرعت کوانتوم در پوسته به c می رسد. این رویدادی مشابه جهان ماست که ثابت هابل متفاوت دارد.
خواهیم داشت:
معادله ۱۲
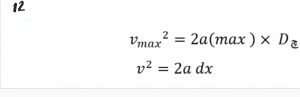
تفسیر معادله بالا اینطور است:
سوژه تحت شتاب a در زمان چt فاصله dx را میپیماید.ما فاصله مبدا ساکن حاوی جرم m و سوژه متحرک را برابرdx میگیریم.
همچنین میتوان گفت سوژه تحت شتاب حداکثرa(max) در زمان چt فاصله چD را می پیماید.
( و همچنین میتوان گفت که dx معادل فاصلهای است که سوژه تحت شتاب حداکثر، در زمان فرضی tx میپیماید.)
همانند آنچه درباره نسبیت خاص گفته شد، این بار سرعت را به شتاب تبدیل می کنیم. در این حالت سرعت فرضی v را میتوان به جای شتاب ، به سوژه نسبت داد:
dx معادل فاصله ای است که سوژه با حداکثر سرعت فرضی(ناشی از شتاب) ، در زمان چD طی میکند.
ضریب نسبیتی اینطور بیان میشود:
معادله ۱۳

در مورد شتاب گرانشی داریم:
معادله ۱۴
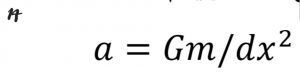
** این همان نتیجه انبساط زمانی نسبیت عام را بیان می کند: dx در این حالت نشان دهنده فاصله طی شده فرضی توسط سوژه در اثر شتاب است.
معادله ۱۵
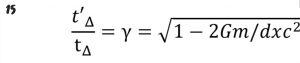
**در مورد شتاب کولونی داریم:
معادله ۱۶
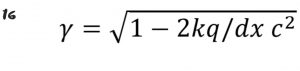
درشکل ۴_د تصویر دایره های رویداد گرانش جرم m بر سوژه ای در فاصله dx را میبینید.
شکل۴_د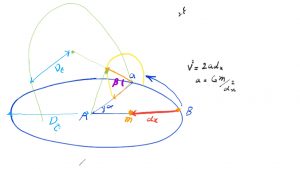
• ساختار هندسی که توصیف شد، براساس ساختار چهاربعدی خاصی در ریاضیات مدرن است که بعدا توصیف می شود.
• تناظر بردارهای (فضایی_زمانی) شعاعی و چرخشی بر اساس “قضیه هلمهوتز ” است که بعدا تشریح می شود.
• بررسی ساختار پیش هندسی فضا-زمان، هم اکنون در نوک پیکان تحقیقات حوزه گرانش کوانتومی و ریسمان است. از جمله پیشروها در این زمینه ” نیما حامد ارکانی” است.
• امکان وجود دو بعد زمانی علاوه بر نظریات “کالوزا-کلاین”، امروزه توسط دانشمندانی چون ” کامران وفا” بررسی می شود.
جمع بندی:
اطلاعات اولیه (اطلاعات درونی رویداد) که همه ناظرها درباره آن اتفاق نظر دارند، شامل اطلاعات شعاعی در دایرههای رویداد است :
۱- طول عمر _ شعاع جهان: چD و چt
2-سرعت حداکثر : c = Vmax= چt/چD
۳- سرعتv_ شتاب a سوژه(شتاب که بر اساس سرعت فرضی تحلیل می شود)
حال، بر اساس سرعت سوژه( که مانند نسبیت، همه ناظرها درباره آن توافق دارند) بازه زمانی و مکانی رویداد درحال وقوع(txوdx)، قابل تعریف است:
چv/c=tx/t
dx/tx=c
tx , dx اطلاعات درونی رویداد هستند. اطلاعات ظاهری اولیه. ناظر dx را بعنوان بازه جابجایی در نظر می گیرد( مثلا مقدار حرکت سوژه با سرعت v و یا فاصله سوژه تحت تاثیر شتاب با سوژه ساکن که شتاب را با جرم- بار الکتریکی ایجاد کرده)
تا اینجا همه ناظرها درباره اطلاعات سه گانه که گفته شد، توافق دارند. توجه کنید که هنوز درباره آنچه هر ناظر درک می کند حرفی نزدهایم. زمان و جابجایی ذکر شده، در مرحله پیش هندسی اولیه و بر اساس اطلاعات پایه سه گانه تعریف می شوند. گذر زمان و بازه مکانی که توسط ناظر ادراک میشود، ( d و tΔ) حاصلضرب برداری میان زیربردارهای tx,z و dx,z است. تنها در مرحله ادراکی است که زمان به عنوان اطلاعات دریافت می شود.
در بخش آینده درباره ضریب نسبیتی دیگری خواهیم گفت که در محاسبات به کارمان خواهد آمد.
ادامه دارد »»»
نویسنده: دکتر حامد شهابی

 (6 نفر , میانگین : 4,17 از 5)
(6 نفر , میانگین : 4,17 از 5)







نظریه شما مفهوم لختی را چگونه توضیح می ده؟
سلام ،دکتر شهابی لینک کتابتونو گذاشته بودین یا من اشتباه میکنم ؟
سلام.کتاب هنوز چاپ نشده. اطلاع میدم
با سپاس…
در کل شما این فرضیه را بر اساس ناظر و اتفاق در حال انجام ترتیب دادید ولی هنوز نمی تونم اینکه چگونه از داخل این موارد زمان را استخراج کردید را درک کنم لطفا اگر اشتباه می کنم به من کمک کنید.
سلام.
اطلاعات اولیه (اطلاعات درونی رویداد) که همه ناظرها درباره آن اتفاق نظر دارند، شامل اطلاعات شعاعی در دایره های رویداد است :
۱.طول عمر _ شعاع جهان: چD و چt
2.سرعت حداکثر : c = Vmax= چt/چD
۳. سرعتv_ شتاب a سوژه(شتاب که بر اساس سرعت فرضی تحلیل میشود)
حال ،بر اساس سرعت سوژه( که مانند نسبیت ، همه ناظرها درباره آن توافق دارند)بازه زمانی و مکانی رویداد درحال وقوع(txوdx)، قابل تعریف است:
چv/c=tx/t
dx/tx=c
tx , dx اطلاعات درونی رویداد هستند.اطلاعات ظاهری اولیه. ناظر dx را بعنوان بازه جابجایی در نظر میگیرد( مثلا مقدار حرکت سوژه با سرعت v و یا فاصله سوژه تحت تاثیر شتاب با سوژه ساکن که شتاب را با جرم- بار الکتریکی ایجاد کرده)
تا اینجا همه ناظرها درباره اطلاعات سه گانه که گفته شد،توافق دارند.توجه کنید که هنوز درباره آنچه هر ناظر درک میکند حرفی نزده ایم. زمان و جابجایی ذکر شده ، در مرحله پیش هندسی اولیه و بر اساس اطلاعات پایه سه گانه تعریف میشوند.
گذر زمان و بازه مکانی که توسط ناظر ادراک میشود، ( d و
tΔ) حاصلضرب برداری میان زیربردارهای tx و dx است.
تنها در مرحله ادراکی است که زمان به عنوان اطلاعات دریافت میشود.
آنچه
واقعا ممنون از راهنماییتون
ممنون از پرسش روشنگرانه شما. پاسخ را به پایان بخش سوم اضافه خواهم کرد.
ای کاش می شد این فرضیه یا به عبارتی این گام نو در توضیح مفاهیم پایه ای فیزیک را به شکلی قابل فهم تر نگاشت ! چیزی شبیه « تاریخ مختصر زمان » !
واقعیت این است که فرمول بندی های ریاضی را نه همه ی خواص ، بلکه خواصی مخصوص می توانند حلاجی کنند !
این را هم می دانم که شاید غیراز این چاره ای نباشد ! زبان زبان ریاضی ست …
سلام.باور کنید من تمام سعیم را کرده ام که به زبان شیوا مطالب پیچیده را بیان کنم. ناشیوایی کلام مرا ببخشید. ولی ریاضیات تنها زبان توصیف مناسب و شیوا خواهد بود.
در بخشهای آینده ، بدون ابزار ریاضی ،گام به گام به مرز جنون نزدیک میشویم .درک ساختار چهار بعدی، دینامیک و استاتیک کوانتومهای <ژ> ،رمز نگاری و رمزگشایی جهان توسط ناظر، ترمودینامیک اطلاعات ، نقش بوزون هیگز، جهان به عنوان سیاهچاله ، و.. مشکل ولی به شدت جذاب است.
با من همراه باشید و مطلب را با دوستان، دانشجویان و اساتیدی که میشناسید به اشتراک بگذارید.
یک نظریه درست یا حتی فرضیه درست مثل یک دستگاهی می مونه که فرکانس خاصی از امواج را مشاهده می کنه یعنی هر نظریه ای یک عینکی هست که با اون جهان رو می بینیم و بعضی حقایق برامون روشن میشه اما فرضیه شما یک عینک نیست بلکه مثل یک تور سبز می مونه که جهان رو پیچیده تر و غیرواقعی نشون میده و اصولا از نبوغ در کشف یک حقیقت کوچک خالی است ولی فرضیه شما حرکتی است انقلابی . درسته که فرضیه کلا مشکل خاصی رو حل نمیکنه ولی حداقل بهمون میگه که راهی که فرضیه رفته رو نباید بریم. به امید روزی که اون حقیقت کوچیک به ذهنتون برسه و یک عینک به جامعه بشری هدیه کنید
سلام. چند روز پیش مطلب جالبی در این وبسایت ارائه شد:
“شاید برای اندازهگیری انبساط کیهان به فیزیک جدیدی نیاز باشد”http://bigbangpage.com/?p=74021
از اتفاق در این فرضیه مقدار دقیقی برای ثابت هابل بدست میاید. ۷۰ مگاپارسک بر ثانیه!
غیر از این ،فرضیه مشکلات خاص تری را حل میکند:
منشا ماده تاریک ، انرژی تاریک ، مقدار ثابت ساختار ریز، اندازه جهان ، دمای خلا، فرکانس تابش CBM، مقدار بار الکتریکی پایه، تحلیل آزمایش دو شکاف یانگ، مقدار شعاع الکترون ، پروتون و اتم هیدروژن ، مساله شعاع پروتون و…
عجول نباشید.
سلام ودرود. کاملا درست گفتین. نظریه بدون ریاضیات ،نمیتواند جهانی را که در آن هستیم، تفسیر کند. استحاله میشود به یک بیانیه شبه فلسفی.
کتابی با بیش از ۵۰۰ صفحه و حاوی معادلات زیاد، عموما خواننده را دلزده میکند. از اینرو چند بخش اول را برای آشنایی به مرور منتشر خواهیم کرد تا خواننده، مشتاق بررسی بیشتر شود.
با کمک وبسایت علمی بیگ بنگ ، کتاب تا چند وقت دیگر منتشر خواهد شد.
مقاله میتونه چیز جالبی باشه ولی بهترست همشو در یک جا و در یک زمان ارائه بدین.و صد البته با معادلات و اساس ریاضی فرضیه.(یا شاید بهتر بگم یک تعبیر)مقاله میتونه چیز جالبی باشه ولی بهترست همشو در یک جا و در یک زمان ارائه بدین.و صد البته با معادلات و اساس ریاضی فرضیه.(یا شاید بهتر بگم یک تعبیر)یک فرضیه نظریه و حتی یک تعبیر نو از دستاوردهای پیشینیان باید بر یک ریاضیات محکم و استوار تکیه کنه و با غنای عمیق ابزارهای ریاضی بتواند به نتایج تازه ای(البته با تایید مشاهدات) احتمالا برسد.
بسیار جالب
با تشکر